Overivew

本文将介绍Guided Policy Search(GPS)这种Model-Based的强化学习算法，并会按以下方式展开：

Motivation：介绍GPS这种方法的特点；
Problem formulation：介绍GPS所解决问题的具体形式；
Framework：介绍GPS的整体框架；
Deterministic policy case：从相对简单的deterministic policy case开始介绍GPS的具体流程；
Stochastic policy case：从deterministic policy case过渡到stochastic policy case，介绍完整的GPS算法。

Motivation

下面通过将GPS跟不同类型的算法进行比较来说明GPS的特点。

与Model-Free算法相比：由于GPS对环境建立了模型（i.e., model/dynamics），在计算q value时，不仅仅是“记录”，还能进行“推算”，因此sample efficiency会比较高，收敛速度会比较快；
与其他Model-Based算法相比：在test的时候，部分Model-Based算法需要进行online optimization（i.e., 根据当前拟合的模型，使用某种优化算法，得到当前的action）；而由于GPS最终得到的是一个parametric policy（e.g., 神经网络），因此在test的时候会比较快（无需做online optimization，只需要做一次forward pass）；
与简单的Imitation Learning算法相比：在简单的IL中，teacher单方面地给student传授知识（i.e., supervised learning），而不管student的学习能力如何；而在GPS中，除了teacher给student传授知识以外，student还会给teacher反馈，要求teacher适配student的学习能力，形成闭环，因此train的效果会更好。

Problem Formulation

下面对我们所讨论的问题做一个界定。

setting
- fixed time length task（e.g, 完成任务的时长限定在20s内，决策的频率是20Hz，则总步长$T$为400）
assumption
- deterministic dynamics：$x_t = f(x_{t-1}, u_{t-1})$
input
- environment
- immediate cost(reward) function：$c(x_t, u_t)$
output
- parametric policy
  - deterministic case：$u_t = \pi_\theta(x_t)$
  - stochastic case：$\pi_\theta(u_t \vert x_t) \sim \mathcal{N}(\mu_t, \Sigma_t)$

Framework

下面介绍GPS的整体框架。

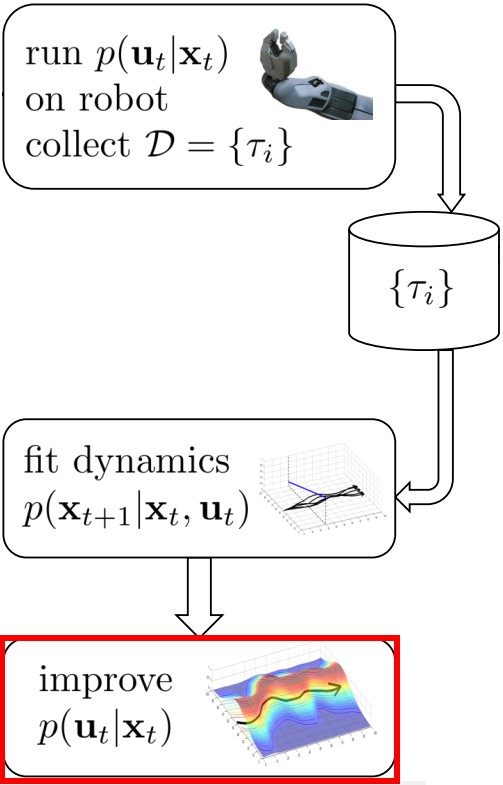
collect data：通过controller与environment进行交互，收集数据；
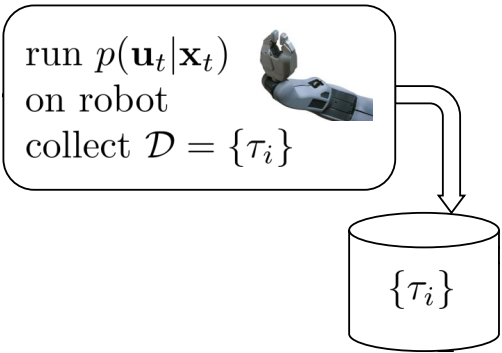
fit dynamics：根据第一步收集到的数据，拟合dynamics；
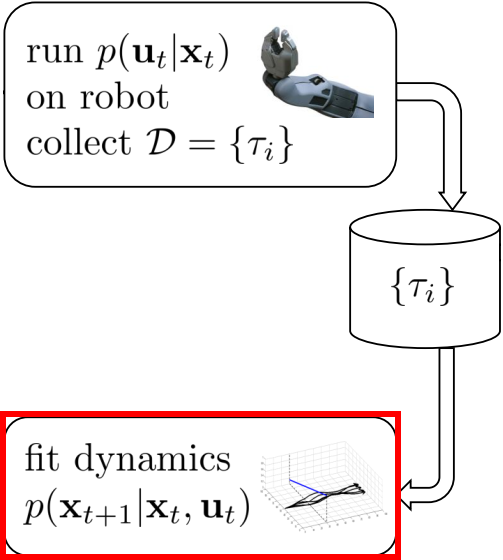
optimization：优化controller（最优控制器）与policy（最终输出的parametric policy）；
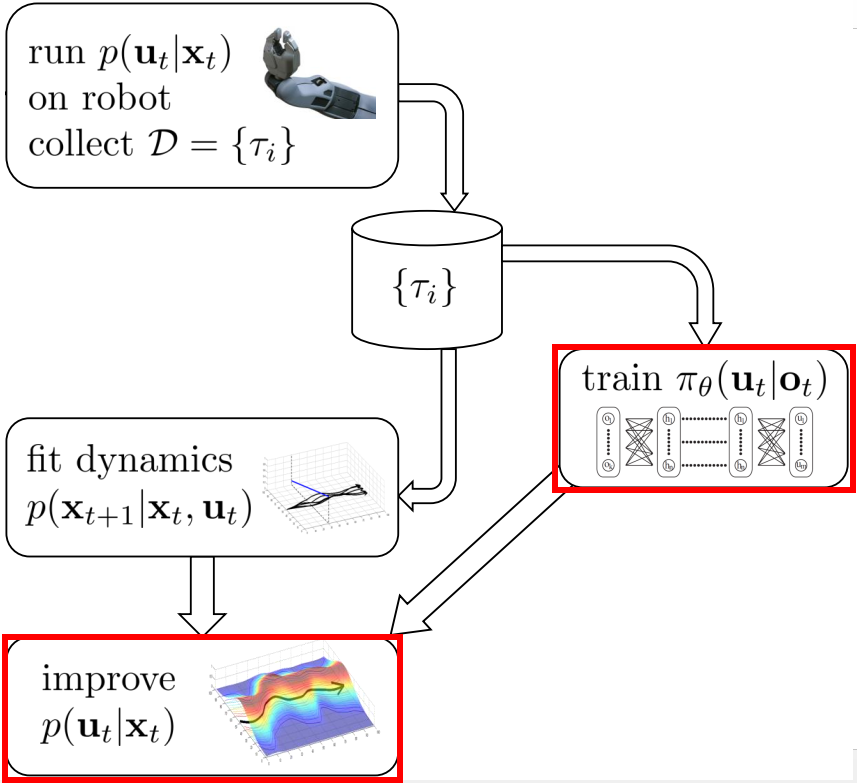
next iteration：迭代。

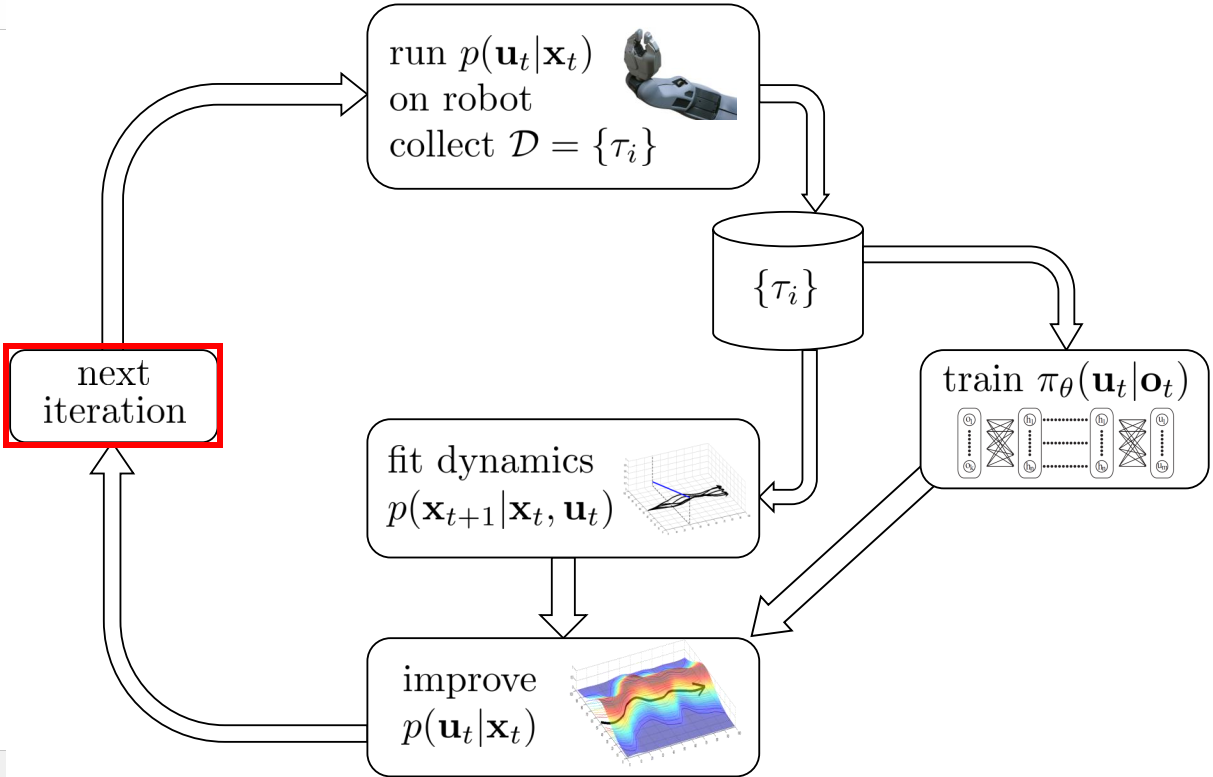
Deterministic policy case

下面开始介绍Deterministic policy case下GPS的具体流程。

Collect data

使用controller与environment进行交互，得到轨迹数据集$\mathcal{D} = { \tau_i }$，其中轨迹$\tau_i = { x_{1i}, u_{1i}, \dots , x_{1T}, u_{1T} }$。

Fit dynamics

使用第一步得到的轨迹数据集来拟合一个time-varying linear model：$x_{t+1} = f(x_t, u_t) = A_tx_t + B_tu_t + c_t$，也就是说这个model对于不同时刻$t$的input会使用不同的linear model。

具体的拟合方法是使用同一时刻$t$，不同轨迹$\tau_i$的数据${ (x_{t1}, u_{t1}, x_{t+1,1}), \dots , (x_{ti}, u_{ti}, x_{t+1,i}) }$来做linear regression。

Optimization

Controller

big picture

optimization problem
- 我们想要在满足dynamics约束的条件下，最小化总cost，因此对应的轨迹优化问题为：
  $$
  \begin{aligned}
  \mathop{\text{min }}_{x_1, u_1, \dots, x_T, u_T} &\sum_{t=1}^T c(x_t, u_t) \\
  \text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
  \end{aligned}
  $$
solution
- 假如上述轨迹优化问题中$f(x_t, u_t) = F_t \begin{bmatrix} x_t \\\ u_t \end{bmatrix} + f_t$， $c(x_t, u_t) = \frac{1}{2} \begin{bmatrix} x_t \\\ u_t \end{bmatrix}^T C_t \begin{bmatrix} x_t \\\ u_t \end{bmatrix} + \begin{bmatrix} x_t \\\ u_t \end{bmatrix}^T c_t$，则有一个叫做Linear Quadratic Regulator(LQR)的优化方法可以对该轨迹优化问题进行求解。
- LQR基本原理如下：
  - input：
    - linear model（$F_t, f_t$）
    - quadratic cost（$C_t, c_t$）
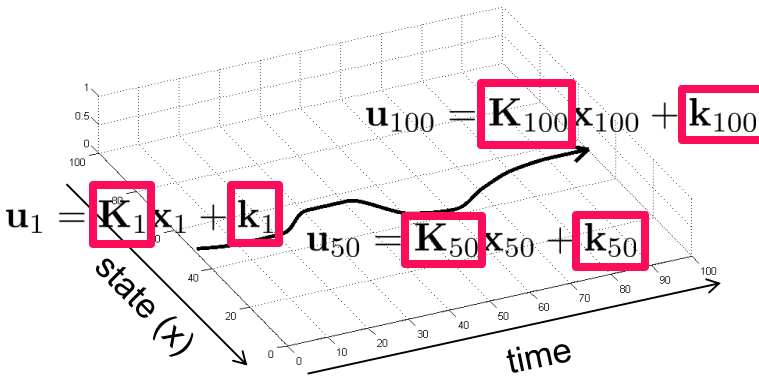
  - output：$K_t, k_t$
  - optimal control（上述轨迹优化问题的解）：$u_t=K_tx_t+k_t$，$x_{t+1}=f(x_t, u_t)$
- 由于我们在fit dynamics中拟合的就是一个linear model，因此只要我们设置的cost function是quadratic的话就可以使用LQR来求解。
- 即使我们的cost function不是quadratic，也还可以使用iterative LQR(iLQR)来进行求解。iLQR可以求解nonlinear dynamics，nonquadratic cost下的轨迹优化问题，它的核心思想是对dynamics和cost分别进行linear及quadratic展开，然后用LQR进行求解。

Policy

big picture

optimization problem
- 因为GPS最后想要的是一个policy，因此在上述轨迹优化问题的基础上，加上一个优化变量$\theta$以及约束条件$u_t = \pi_\theta(x_t)$，来表示我们希望policy能够“学习”optimal control：
  $$
  \begin{aligned}
  \mathop{\text{min }}_{x_1, u_1, \dots, x_T, u_T, \theta} &\sum_{t=1}^T c(x_t, u_t) \\
  \text{s.t. } &u_t = \pi_\theta(x_t) \quad t=1, \dots, T\\
  &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
  \end{aligned}
  $$
solution
- 求解上述优化问题用到了一种叫做Dual Gradient Descent(DGD)的优化方法。DGD是一种求解形如以下优化问题的方法：
  $$
  \begin{aligned}
  \mathop{\text{min }}_x &f(x) \\
  \text{s.t. } & C(x)=0.
  \end{aligned}
  $$其具体求解过程为：
  1. 写出对应的Lagrangian函数：$\mathcal{L}(x, \lambda) = f(x) + \lambda C(x)$；
  2. 求解最小化Lagrangian函数的$x$：$x^* = \mathop{\text{argmin }}_x \mathcal{L}(x, \lambda)$；
  3. 将$x^*$代入$\mathcal{L}(x, \lambda)$得到原问题的下界函数$g(\lambda) = \mathcal{L}(x^*, \lambda)$；
  4. 更新$\lambda$（类似对$\lambda$做gradient ascent）：$\lambda = \lambda + \alpha \frac{\partial g}{\partial \lambda}$；
  5. 回到第二步，求新$\lambda$下对应的$x^*$，迭代。
- 接下来改变一下优化问题的表述方式，将dynamics约束单独提出来（之所以这么做，是为了将问题化归为会解的问题，下面会详细说），也就是说现在把问题理解为在满足dynamics约束下求解一个约束优化问题（i.e., 满足policy约束下最小化cost），而原来是满足dynamics和policy约束下求解一个无约束优化问题（i.e., 最小化cost）：
  $$
  \begin{aligned}
  \mathop{\text{min }}_{x_1, u_1, \dots, x_T, u_T, \theta} &\sum_{t=1}^T c(x_t, u_t) \\
  \text{s.t. } &u_t = \pi_\theta(x_t) \quad t=1, \dots, T\\
  \\
  \text{s.t. } x_t = f&(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
  \end{aligned}
  $$
- 然后进行约束条件下的DGD（i.e., 整个DGD的过程都要满足约束）：
  1. 仅将policy约束写进Lagrangian函数：
    $$
    \begin{aligned}
    \mathcal{L}(\tau, \theta, \lambda)
    &= \mathcal{L}(x_1, u_1, \dots, x_T, u_T, \theta, \lambda_1, \dots, \lambda_T) \\
    &= \sum_{t=1}^T c(x_t, u_t) + \sum_{t=1}^T\lambda_t [u_t - \pi_\theta(x_t)] \\
    &= \sum_{t=1}^T { c(x_t, u_t) + \lambda_t [u_t - \pi_\theta(x_t)] }.
    \end{aligned}
    $$
  2. 本来应该将$\begin{bmatrix}\tau \\\ \theta\end{bmatrix}$这一整个向量看作优化变量（对应DGD中的$x$），然后求解$\begin{bmatrix}\tau \\\ \theta\end{bmatrix}^*$（对应DGD中的$x^*$）。但这里假设$\tau$和$\theta$相互独立（为了能够求解），因此下面可以分别单独对$\tau$与$\theta$做优化，求得对应的$\tau^*$和$\theta^*$，然后用$\begin{bmatrix}\tau^* \\\ \theta^*\end{bmatrix}$来近似$\begin{bmatrix}\tau \\\ \theta\end{bmatrix}^*$。
  3. 求解$\tau^*$：对应的优化问题为：
    $$
    \begin{aligned}
    \mathop{\text{min }}_\tau &\sum_{t=1}^T { c(x_t, u_t) + \lambda_t [u_t - \pi_\theta(x_t)] } \\
    \text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
    \end{aligned}
    $$设$\tilde{c}(x_t, u_t)=c(x_t, u_t) + \lambda_t [u_t - \pi_\theta(x_t)]$，我们有：
    $$
    \begin{aligned}
    \mathop{\text{min }}_\tau &\sum_{t=1}^T \tilde{c}(x_t, u_t)\\
    \text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
    \end{aligned}
    $$而这个形式的优化问题我们能够通过iLQR进行求解，因此能够求得$\tau^*$。
  4. 求解$\theta^*$：对应的优化问题为：
    $$
    \begin{aligned}
    \mathop{\text{min }}_\theta &\sum_{t=1}^T { c(x_t, u_t) + \lambda_t [u_t - \pi_\theta(x_t)] } \\
    \text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
    \end{aligned}
    $$由于优化变量是$\theta$，所以约束条件可以去掉，而且目标函数也可以简化，等价的优化问题为：
    $$
    \begin{aligned}
    \mathop{\text{min }}_\theta &\sum_{t=1}^T \lambda_t [u_t - \pi_\theta(x_t)].
    \end{aligned}
    $$这是一个无约束优化问题（带权拟合问题），可以用诸如SGD等方法进行优化，因此也能够求得$\theta^*$。
  5. 将$\tau^*$和$\theta^*$代入Lagrangian函数，得到$g(\lambda) = \mathcal{L}(\tau^*, \theta^*, \lambda)$。
  6. 对$\lambda$做单步gradient ascent（跟求解$\theta^*$时一样，由于约束条件跟优化变量无关，所以等价于无约束优化），更新$\lambda$，迭代。

Next iteration

回到第一步collect data，即用新的controller跟environment交互，迭代。

Summary

至此我们已经通过相对简单的deterministic policy case过了一遍GPS的整个流程，下面补充一些小小的细节：

为什么称之为GPS：guided主要体现在最后优化问题的约束$u_t = \pi_\theta(x_t)$，相当于有一个teacher（controller）在“指引”我们的policy。
collect data使用controller还是policy：应该是使用controller，因为policy仅仅拟合了某些具体的$(x_t, u_t)$，而controller对各个$x_t$都是“最优”的。
为什么流程图中，train policy部分会跟$\tau_i$相关：这是因为在求解$\theta^*$时，$\tau^*$还没代入Lagrangian函数，也就是说Lagrangian函数中用的是$\tau$而不是$\tau^*$。

Stochastic policy case

deterministic controller对于一个起始点只能采集到一条轨迹，不利于拟合一个robust的dynamics，因此我们想要一个stochastic的controller。之后通过对stochastic controller进行supervised learning，我们最后会得到一个stochastic policy。

stochastic policy case跟deterministic policy case的唯一区别在于optimization这步（如红框所示），其他都是一样的。因此下面仅介绍stochastic policy case如何做optimization。

Using stochastic controller

首先介绍一个过渡性的内容，是关于使用stochastic controller的。

最直观的想法：把原来的约束问题（暂时先不考虑policy）改一下，将controller表示为$p(u_t \vert x_t) \sim \mathcal{N}(\mu_t, \Sigma_t)$，然后求解优化问题：
$$
\begin{aligned}
\mathop{\text{min }}_{\tau, p} &\mathbb{E}_\tau[\sum_{t=1}^T c(x_t, u_t)] \\
\text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T,
\end{aligned}
$$其中$p = \mu_1, \Sigma_1, \dots, \mu_T, \Sigma_T$。但这样子是不work的，因为最后求出来的还是一个determinisitc controller（因为贪婪地采取最优策略效果是最好的）。
于是就强行把controller设成linear-gaussian的形式：
$$
p(u_t \vert x_t) = \mathcal{N}(K_t(x_t - \hat{x}_t) + k_t + \hat{u}_t, Q^{-1}_{u_t,u_t}),
$$其中，gaussian的均值为iLQR的解，方差为iLQR中的某个矩阵的逆，具体含义可以不用管，只需要知道这些东西都可以通过iLQR得到。
而该形式的controller恰好是以下优化问题的最优解：
$$
\begin{aligned}
\mathop{\text{min }}_{\tau, p} &\sum_{t=1}^T\mathbb{E}_{p(x_t, u_t)}[ c(x_t, u_t) - \mathcal{H}(p(u_t \vert x_t))] \\
\text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
\end{aligned}
$$
这部分主要为下面做铺垫，核心在于我们现在知道了某种形式的优化问题的最优解。

Constrain controller in trust region

motivation
- 在GPS中我们所fit的dynamics是local dynamics，也就是说它仅在当前controller“附近”是有效的；
- 在优化问题中，我们评价controller好坏会用到该local dynamics；
- 因此，为了确保评价的有效性，我们要限定controller在当前controller“附近”；
- 否则，即使contoller评价很高，也是虚假的/无效的/没有意义的。
solution
- 将controller在当前controller“附近”用数学语言表述出来，即
  $$
  D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) \leq \epsilon,
  $$其中$p(\tau)$表示轨迹$\tau$在新controller下发生的概率，$\bar{p}(\tau)$表示轨迹$\tau$在当前controller下发生的概率，$D_{KL}$表示KL-divergence，用于衡量两个分布的“相似程度”，KL-divergence越小，两个分布越相似。
  - 这个表示能够间接地限制controller和当前controller比较相似，因为$p(\tau) = p(x_1)\prod_{t=1}^{T-1} p(u_t \vert x_t)f(x_{t+1} \vert x_t, u_t)$，而对于新旧controller来说，$p(x_1)$以及$f(x_{t+1} \vert x_t, u_t)$都是一样的，因此区别仅仅在于$p(u_t \vert x_t)$。换句话说，$p(\tau)$和$\bar{p}(\tau)$的区别仅仅在于controller，因此控制$p(\tau)$和$\bar{p}(\tau)$的相似程度就可以间接地控制controller的相似程度。
- new optimization problem
  $$
  \begin{aligned}
  \mathop{\text{min }}_{\tau, p} &\mathbb{E}_\tau[\sum_{t=1}^T c(x_t, u_t)] \\
  \text{s.t. } &D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) \leq \epsilon \\
  &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
  \end{aligned}
  $$
- 进行约束条件下的DGD（这里我不太懂为什么可以对不等式约束做DGD，逻辑上来讲对于不等式约束，需要限定$\lambda \geq 0$才能保证$g(\lambda)$是原问题的下界函数）：
  1. 仅将$D_{KL}$约束写进Lagrangian函数：
    $$
    \begin{aligned}
    \mathcal{L}(\tau, p, \lambda) &= \mathbb{E}_\tau[\sum_{t=1}^T c(x_t, u_t)] + \lambda (D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) - \epsilon) \\
    &// D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) = \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)} [- \log \bar{p}(u_t \vert x_t) - \mathcal{H}(p(u_t \vert x_t))] \\
    &= \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[c(x_t, u_t) - \lambda \log \bar{p}(u_t \vert x_t) - \lambda \mathcal{H}(p(u_t \vert x_t))] - \lambda \epsilon \\
    &//提\lambda \\
    &= \lambda \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[\frac{1}{\lambda} c(x_t, u_t) - \log \bar{p}(u_t \vert x_t) - \mathcal{H}(p(u_t \vert x_t))] - \epsilon
    \end{aligned}
    $$
  2. 求解$\begin{bmatrix} \tau \\\ p \end{bmatrix}^*$：对应的优化问题为：
    $$
    \begin{aligned}
    \mathop{\text{min }}_{\tau, p} &\sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[\frac{1}{\lambda} c(x_t, u_t) - \log \bar{p}(u_t \vert x_t) - \mathcal{H}(p(u_t \vert x_t))] \\
    \text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
    \end{aligned}
    $$假如我们设$\tilde{c}(x_t, u_t) = \frac{1}{\lambda} c(x_t, u_t) - \log \bar{p}(u_t \vert x_t)$，则该优化问题为：
    $$
    \begin{aligned}
    \mathop{\text{min }}_{\tau, p} &\sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[\tilde{c}(x_t, u_t) - \mathcal{H}(p(u_t \vert x_t))] \\
    \text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
    \end{aligned}
    $$而这个形式的优化问题我们知道其最优解的形式是什么（回忆Using stochastic controller部分），因此我们能够用iLQR求解$\begin{bmatrix} \tau \\\ p \end{bmatrix}^*$。
  3. 对$\lambda$做单步gradient ascent，迭代。

Introduce stochastic policy

statement
- 这部分由于没有细看论文，所以有些地方我也不是很清楚，只是介绍我自己的理解，希望谅解：）。
motivation
- 我们想要得到的是一个parametric policy，因此采用跟deterministic policy case一样的思路，添加一个policy约束。
solution
- optimization problem
  $$
  \begin{aligned}
  \mathop{\text{min }}_{\tau, p} &\mathbb{E}_\tau[\sum_{t=1}^T c(x_t, u_t)] \\
  \text{s.t. } &p(u_t \vert x_t) = \pi_\theta(u_t \vert x_t) \quad t=1, \dots, T \\
  &D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) \leq \epsilon \\
  &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
  \end{aligned}
  $$
- 进行约束条件下的DGD：
  1. 仅将policy约束和$D_{KL}$约束写进Lagrangian函数：
    $$
    \begin{aligned}
    \mathcal{L}(\tau, p, \theta, \lambda, \eta) &= \mathbb{E}_\tau[\sum_{t=1}^T c(x_t, u_t)] + \sum_{t=1}^T \lambda_t [p(u_t \vert x_t) - \pi_\theta(u_t \vert x_t)] + \eta (D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) - \epsilon) \\
    &// \sum_{t=1}^T \lambda_t [p(u_t \vert x_t) - \pi_\theta(u_t \vert x_t)] \overset{?}{\approx} \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[u_t^T\lambda_t + \rho_t D_{KL}(p(u_t \vert x_t) \Vert \pi_\theta(u_t \vert x_t))]\\
    &\approx \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[c(x_t, u_t) + u_t^T\lambda_t + \rho_t D_{KL}(p(u_t \vert x_t) \Vert \pi_\theta(u_t \vert x_t))] + \eta (D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) - \epsilon) \\
    &// \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[D_{KL}(p(u_t \vert x_t) \Vert \pi_\theta(u_t \vert x_t))] = \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[- \log \pi_\theta(u_t \vert x_t) - \mathcal{H}(p(u_t \vert x_t))] \\
    &// D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) = \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)} [- \log \bar{p}(u_t \vert x_t) - \mathcal{H}(p(u_t \vert x_t))] \\
    &= \sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[c(x_t, u_t) + u_t^T\lambda_t - \rho_t \log\pi_\theta(u_t \vert x_t) - \eta \log \bar{p}(u_t \vert x_t) - ( \rho_t + \eta) \mathcal{H}(p(u_t \vert x_t))] - \eta \epsilon
    \end{aligned}
    $$
  2. 求解$\begin{bmatrix} \tau \\\ p \end{bmatrix}^*$：对应的优化问题为：
    $$
    \begin{aligned}
    \mathop{\text{min }}_{\tau, p} &\sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[c(x_t, u_t) + u_t^T\lambda_t - \rho_t \log\pi_\theta(u_t \vert x_t) - \eta \log \bar{p}(u_t \vert x_t) - ( \rho_t + \eta) \mathcal{H}(p(u_t \vert x_t))] \\
    \text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
    \end{aligned}
    $$设$\tilde{c}(x_t, u_t) = c(x_t, u_t) + u_t^T\lambda_t - \rho_t \log\pi_\theta(u_t \vert x_t) - \eta \log \bar{p}(u_t \vert x_t)$，$\nu_t = \rho_t + \eta$，则上述优化问题可以表示为：
    $$
    \begin{aligned}
    \mathop{\text{min }}_{\tau, p} &\sum_{t=1}^T \mathbb{E}_{p(x_t, u_t)}[\tilde{c}(x_t, u_t) - \nu_t \mathcal{H}(p(u_t \vert x_t))] \\
    \text{s.t. } &x_t = f(x_{t-1}, u_{t-1}) \quad t=1, \dots, T.
    \end{aligned}
    $$而这个形式的优化问题我们知道最优解（回忆Using stochastic controller和Constrain controller in trust region部分），因此得到$\begin{bmatrix} \tau \\\ p \end{bmatrix}^*$。
  3. 求解$\theta^*$：跟deterministic policy case一样，由于约束条件跟待优化变量无关，所以实际上是一个无约束优化问题，不过问题是这里并没有用直接用上面的Lagrangian函数，我猜测问题是出在上面我没搞懂的带问号的约等于号那里，也许上面只是为了求解方便做了近似，因此在求解$\theta^*$时没有把Lagrangian函数展开到最后的形式，而是用了以下Lagrangian函数：
    $$
    \begin{aligned}
    \mathcal{L}(\tau, p, \theta, \lambda, \eta) &= \mathbb{E}_\tau[\sum_{t=1}^T c(x_t, u_t)] + \sum_{t=1}^T \lambda_t [p(u_t \vert x_t) - \pi_\theta(u_t \vert x_t)] + \eta (D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) - \epsilon) \\
    &// \sum_{t=1}^T \lambda_t [p(u_t \vert x_t) - \pi_\theta(u_t \vert x_t)] \overset{?}{=} \sum_{t=1}^T \mathbb{E}_{p(x_t)}[\mathbb{E}_{\pi_\theta(u_t \vert x_t)}[u_t]^T\lambda_t + \rho_t D_{KL}(p(u_t \vert x_t) \Vert \pi_\theta(u_t \vert x_t))]\\
    &= \mathbb{E}_\tau[\sum_{t=1}^T c(x_t, u_t)] + \sum_{t=1}^T \mathbb{E}_{p(x_t)}[\mathbb{E}_{\pi_\theta(u_t \vert x_t)}[u_t]^T\lambda_t + \rho_t D_{KL}(p(u_t \vert x_t) \Vert \pi_\theta(u_t \vert x_t))] \\
    &+ \eta (D_{KL}(p(\tau) \Vert \bar{p}(\tau) ) - \epsilon) \\
    \end{aligned}.
    $$因此，对应的关于$\theta$的无约束优化问题为：
    $$
    \mathop{\text{min }}_{\theta}\sum_{t=1}^T \mathbb{E}_{p(x_t)}[\mathbb{E}_{\pi_\theta(u_t \vert x_t)}[u_t]^T\lambda_t + \rho_t D_{KL}(p(u_t \vert x_t) \Vert \pi_\theta(u_t \vert x_t))].
    $$应该可以使用诸如SGD等优化方法进行求解，于是我们得到$\theta^*$
  4. 对$\begin{bmatrix} \lambda \\\ \eta \end{bmatrix}$做单步gradient ascent，迭代。

Conclusion

至此已经介绍完GPS的流程，这个算法给我印象最深刻的地方就是化归的思想，即将新构建的问题转化为之前已经知道解决方法的问题，令人叹为观止。

学习总结《Guided Policy Search》